![[*]](nx_motif.gif)
![[*]](pv_motif.gif)

suivant: Création graphique d'automate
monter: Les automates
précédent: Les automates
Table des matières
Sous-sections
Pour dessiner des automates « à la main », on utilise des courbes pour tracer les liaisons. Pour les faire
dessiner par un programme, la solution peut être d'utiliser des courbes de BEZIER. Elles serviront
uniquement en tant qu'outil ici et ne font donc pas partie intégrante de ce TIPE. Néanmoins, un peu de
théorie et quelques explications semblaient indispensables.
Remarque : Tous les développements théoriques suivants sont tirés du Cours
d'Infographie [5] de Patrick TRAU3.1.
On a souvent besoin de représenter avec l'ordinateur des courbes ou surfaces dont le type n'est soit non
classifiable (ni parabole, ni cercle, ...) soit non connu à l'avance. On les regroupe généralement sous
le nom de « courbes et surfaces non mathématiques », car l'équation mathématique n'est pas connue par le
programmeur. Ces courbes ou surfaces sont en général définies par un ensemble de points, plus ou moins
nombreux.
Le problème qui se posait à la régie RENAULT consistait à représenter les surfaces de
carrosserie dessinées par les designers, pour réaliser les matrices d'emboutissage. La pièce était
définie par des sections planes successives. A l'arrivée des machines à commande numérique, la
méthode manuelle a du être abandonnée. Après création d'une maquette 3D (en bois, plâtre, ...
modifiée au fur et à mesure), la surface était déterminée par une matrice de points obtenus à
l'aide d'une machine à mesurer en 3D. Pour obtenir une bonne précision, le nombre de points nécessaire
est très important. Le nombre de maquettes réalisées en cours de conception étant important (d'où
pertes de temps), on a demandé aux stylistes de créer sur ordinateur, les maquettes pouvant alors être
facilement et rapidement réalisées en commande numérique.
P. BEZIER3.2 a du mettre
au point une méthode permettant de définir la surface par un nombre minimal de points caractéristiques,
permettre de modifier facilement la surface par déplacement d'un minimum de points, pouvoir représenter
toute surface (y compris plane), sans « cassure » (continûment dérivable).
Cette définition de la courbe est possible aussi bien en 2D qu'en 3D. Les
vecteurs 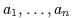 forment le « polygone caractéristique ».
forment le « polygone caractéristique ».
On impose à l'origine (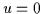 )
:
)
:
- passage en
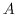 (
( 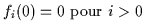 )
)
- la tangente ne dépend que de
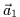 (
( 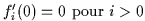 )
)
- la dérivée seconde ne dépend que de
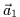 et
et 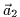 (
( 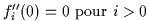 )
)
- de façon générale, la dérivée k-ième ne dépend
que des
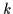 vecteurs
vecteurs 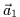 à
à 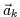
De plus, le dernier sommet du polygone caractéristique impose le point final
de la courbe (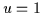 ), la tangente en ce point ne dépend que du dernier vecteur
), la tangente en ce point ne dépend que du dernier vecteur 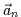 , etc.
, etc.
Exemple : pour 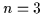 ,
on impose les conditions suivantes :
,
on impose les conditions suivantes :
- passage de la courbe aux deux extrémités du polygone caractéristique :
- la tangente en
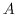 ne dépend que de
ne dépend que de 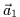 (idem à l'autre extrémité) :
(idem à l'autre extrémité) :
- la dérivée seconde en A ne dépend que de
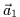 et
et 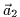 :
:
Plaçons-nous encore dans le cas de trois points : on a 12 conditions. On peut donc prendre trois fonctions du
troisième degré.
Soit 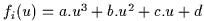 . La dérivée sera donc
. La dérivée sera donc 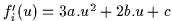 , et la dérivée seconde
, et la dérivée seconde 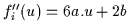 .
.
FIGURE 3.1:
Tracé des fonctions 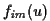 dans le cas
dans le cas 
|
|
Pierre BEZIER a déterminé le cas général (à l'ordre 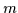 )
:
)
:
Cette seconde écriture se traduit facilement de manière informatique, bien que comportant beaucoup de
calculs.
Plutôt que d'utiliser la formulation vectorielle, on définit le polygone caractéristique
par les coordonnées 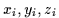 de ses sommets. On obtient les coordonnées de tout point
de la courbe :
de ses sommets. On obtient les coordonnées de tout point
de la courbe :
Pour accélérer les calculs, on cherchera à stocker dans des tableaux les valeurs intermédiaires
réutilisées plusieurs fois pour un tracé. D'autres formulations ont également été développées,
on peut les trouver dans divers ouvrages, par exemple dans la collection Maths et CAO.
On peut définir une courbe complexe avec assez peu de points caractéristiques. Certes la courbe ne passe
pas par ces points, mais avec un peu d'expérience, on « sent » facilement comment déplacer quelques points
caractéristiques pour modifier une courbe. Ceci est encore plus intéressant pour des surfaces
tridimensionnelles, où les modifications elles aussi se limiteront aux déplacements de quelques points.
Ces exemples (cf. FIGURE 3.2) nous montrent la diversité des courbes possibles avec trois ou quatre points.
FIGURE 3.2:
Exemples de courbes de BEZIER
|
|
Pour tracer une courbe de BEZIER, il faut définir le type des points et de la courbe
(cf. PROGRAMME 3.1). Ensuite et pour suivre les conseils précédents, les valeurs des
paramètres, c'est-à-dire les coefficients des polygones caractéristiques, sont stockées dans une
variable globale pour éviter de les recalculer à chaque tracé. C'est la fonction
Cvalues (cf. PROGRAMME 3.2) qui est chargée de ce travail, sachant que l'on
utilisera 100 points pour tracer la courbe. Il ne reste plus alors qu'à tracer la courbe de BEZIER
(cf. PROGRAMME 3.3), en ayant auparavant crée la liste tValues qui contient les valeurs
des paramètres.
PROGRAMME 3.1:
Les types pour les courbes de BEZIER
 |
PROGRAMME 3.2:
Précalcul des paramètres des courbes de BEZIER
![\begin{table}
\begin{verbatim}let CValues nbPts= let Step=1./.nbPts in
let rec...
... ((t3,3.*.t2*.ct,3.*.t*.ct2,ct3)::l)
in rValues 0. [];;\end{verbatim}\end{table}](img88.gif) |
PROGRAMME 3.3:
Tracé des courbes de BEZIER
 |
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)

suivant: Création graphique d'automate
monter: Les automates
précédent: Les automates
Table des matières
1999-01-29
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)
![]() forment le « polygone caractéristique ».
forment le « polygone caractéristique ».
![]() ), la tangente en ce point ne dépend que du dernier vecteur
), la tangente en ce point ne dépend que du dernier vecteur ![]() , etc.
, etc. ![]() ,
on impose les conditions suivantes :
,
on impose les conditions suivantes :
![]() . La dérivée sera donc
. La dérivée sera donc ![]() , et la dérivée seconde
, et la dérivée seconde ![]() .
. 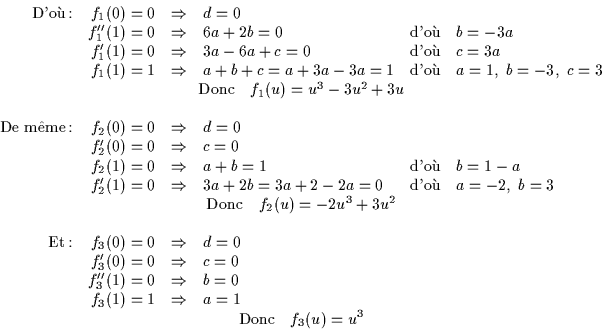
![]() )
:
)
:
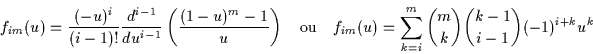
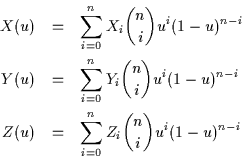
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)