 |
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)
clip_rect qui calcule le plus petit rectangle contenant tous les points (cf. PROGRAMME 11).
Quand l'animation du cube fut terminée, on s'est aperçu que la fonction cree_cube passait beaucoup de
temps à calculer des cosinus et des sinus. Pour y remédier, Il suffisait de les tabuler, c'est-à-dire de
les précalculer et de placer les résultats dans un tableau. Nous n'aurions alors plus qu'à aller lire
les valeurs nécessaires et tous les calculs des sinus et cosinus se transformeraient alors en simple lecture
dans un tableau.
Pour le précalcul, une solution est d'utiliser les formules de TCHEBYTCHEV. Celles-ci permettent grâce
à une formule de récurrence de calculer tous les sinus et cosinus des multiples d'un angle ![]() donné. Il suffit d'initialiser la récurrence avec les deux valeurs du cosinus et du sinus pour les valeurs
0 et
donné. Il suffit d'initialiser la récurrence avec les deux valeurs du cosinus et du sinus pour les valeurs
0 et ![]() .
Ces formules étant assez aisées à établir, nous allons en présenter ici la
démonstration. Celle-ci est basée principalement sur la formule de MOIVRE :
.
Ces formules étant assez aisées à établir, nous allons en présenter ici la
démonstration. Celle-ci est basée principalement sur la formule de MOIVRE :
On exprime alors
![]() et
et
![]() :
:
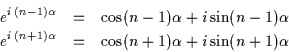
En faisant la somme des ces deux expressions, on obtient alors :
Soit, en factorisant dans le premier membre par
![]() :
:
En prenant partie réelle et partie imaginaire, on obtient :
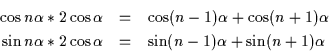
On note alors ![]() la suite des cosinus des multiples entiers de
la suite des cosinus des multiples entiers de ![]() et
et ![]() la suite des sinus des multiples entiers de
la suite des sinus des multiples entiers de ![]() . On obtient alors les relations de récurrence linéaires
d'ordre
. On obtient alors les relations de récurrence linéaires
d'ordre ![]() suivantes :
suivantes :
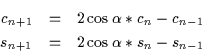
L'avantage de ces formules est double : d'une part, elles sont stables, c'est-à-dire
que les erreurs de calcul successives induites par le calcul réel ne s'amplifient
pas. D'autre part, tous nos angles ne varient que d'une fraction de ![]() à chaque itération. Nous n'avons donc besoin que des valeurs
des sinus et cosinus pour ces fractions de
à chaque itération. Nous n'avons donc besoin que des valeurs
des sinus et cosinus pour ces fractions de ![]() . De plus, en prenant des fractions de
. De plus, en prenant des fractions de ![]() , par exemple
, par exemple ![]() , (ici
, (ici ![]() ,
, ![]() et
et ![]() ), il suffit de calculer les
), il suffit de calculer les ![]() premières valeurs et de reboucler au début du tableau quand
la valeur de l'angle dépasse
premières valeurs et de reboucler au début du tableau quand
la valeur de l'angle dépasse ![]() . Dans la boucle d'animation, à la fin du programme, on calcule
donc les angles modulo
. Dans la boucle d'animation, à la fin du programme, on calcule
donc les angles modulo ![]() . Le précalcul des cosinus et des sinus a été implémenté
comme décrit au PROGRAMME 12
où
. Le précalcul des cosinus et des sinus a été implémenté
comme décrit au PROGRAMME 12
où portion_2Pi est un entier qui définit la fraction de
![]() dont on va calculer les sinus et les cosinus.
dont on va calculer les sinus et les cosinus.
Les tableaux ainsi créés contiendront, à l'indice ![]() , le couple de valeurs de
, le couple de valeurs de ![]() et
et ![]() . On appelle alors trois fois la fonction
. On appelle alors trois fois la fonction calcul_trigo
avant l'exécution.
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)