![[*]](nx_motif.gif)
![[*]](pv_motif.gif)

suivant: Etude de complexité
monter: Modèle « physique »
précédent: Recherche du point frontière
Table des matières
Sous-sections
Soit un point mobile 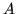 définissant la carte, une « masse »
définissant la carte, une « masse » 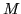 et
et 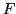 le point frontière (cf. figure 2.1).
On peut alors représenter la situation en dimension 1 (cf. figure 2.2).
Le paramètre
le point frontière (cf. figure 2.1).
On peut alors représenter la situation en dimension 1 (cf. figure 2.2).
Le paramètre 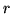 est le rapport des distances
est le rapport des distances 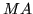 et
et 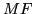 . La nouvelle position du point
. La nouvelle position du point 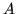 sera donnée par
sera donnée par 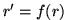 où
où 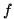 , la loi de déplacement, dépend de la donnée placée
en
, la loi de déplacement, dépend de la donnée placée
en 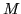 .
.
FIGURE 2.2:
Déplacement d'un point 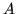
|
|
La première idée est de créer une fonction dont la dérivée
seconde en zéro est proportionnelle à la masse et qui se rapproche de la
première bissectrice lorsque le paramètre 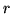 tend vers
tend vers 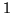 , c'est-à-dire qui n'agit plus à grande distance. Il faut aussi
ajouter les conditions
, c'est-à-dire qui n'agit plus à grande distance. Il faut aussi
ajouter les conditions 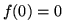 et
et 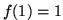 afin que la frontière soit fixe et que la carte garde son aspect
général. Mettons cela en
afin que la frontière soit fixe et que la carte garde son aspect
général. Mettons cela en 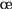 uvre en notant
uvre en notant 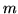 la « masse » du point
la « masse » du point 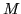 considéré.
considéré.
Soit 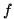 la fonction de classe
la fonction de classe 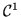 définie sur
définie sur ![$[0;1]$](img24.gif) par :
par :
Il vient alors par une double intégration évidente, tout en s'assurant de
la continuité de 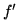 et
et 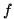 mais aussi que f respecte les conditions
mais aussi que f respecte les conditions 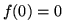 et
et 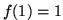 :
:
On obtient alors une famille de fonctions qui semblent convenir (cf. figure 2.3) car elles
satisfont aux conditions qu'on leur avait imposées et qu'elles ont la forme à laquelle on pouvait
s'attendre. Cependant, après quelques tests sur des cas simples, on s'aperçoit que ces fonctions ne
poussent pas suffisamment à proximité des masses. Elles donnent néanmoins certains résultats
satisfaisants dans des situations simples.
FIGURE 2.3:
Première famille de lois de déplacement
|
|
Pour améliorer le résultat précédent, il faut changer de point
de vue sur cette fonction : plutôt que d'imposer des conditions sur la dérivée
seconde, imposons les sur la dérivée en cherchant une fonction ayant
une tangente verticale à l'origine et dont la dérivée vaut 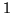 en
en 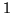 . Soit
. Soit 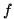 la fonction définie ainsi, en notant toujours
la fonction définie ainsi, en notant toujours 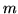 la « masse » du point
la « masse » du point 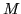 :
:
On peut alors vérifier que cette fonction a les propriétés voulues :
On obtient donc une famille de courbe présentée sur la figure 2.4. Cette fonction est certes
un peu plus lourde que la précédente -- à cause de l'exponentiation -- mais elle donne de
meilleurs résultats sur les quelques tests réalisés et présentés plus loin.
FIGURE 2.4:
Seconde famille de lois de déplacement
|
|
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)

suivant: Etude de complexité
monter: Modèle « physique »
précédent: Recherche du point frontière
Table des matières
1999-10-28
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)
![]() la fonction de classe
la fonction de classe ![]() définie sur
définie sur ![]() par :
par : 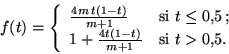
![]() en
en ![]() . Soit
. Soit ![]() la fonction définie ainsi, en notant toujours
la fonction définie ainsi, en notant toujours ![]() la « masse » du point
la « masse » du point ![]() :
: 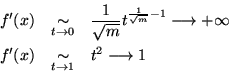
![[*]](nx_motif.gif)
![[*]](pv_motif.gif)